Итак, я пришел к финишной прямой высшего образования. Но кроме длинной дистанции позади, впереди еще маячит заключительное сражение этого триатлона: бакалаврская работа.
В чем проблема? Нужна идея по изменению размера изображения. То есть какая-то модификация стандартного метода, чтобы работало лучше чем оригинал.
Объясняю на пальцах.
Есть картинка и ее увеличение.
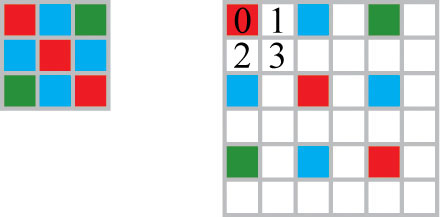
Нужна идея алгоритма, как находить те самые 1ый, 2ой и 3ий пиксель, которых не хватает. Механизм должен быть итерационным (то есть, несколько шагов) и базироваться на сплайн-интерполяции.
Уже испытано 2 метода:
– Сплайн-функцией горизонтальных, вертикальных и диагональных пикселей находятся 1, 2, 3. После чего значение пикселя 0 корректируется в сторону среднего арифметического при помощи некоего коэффициента k. Постулируется то, что среднее арифметическое 0, 1, 2 и 3 должно быть равно исходному значению 0. Результат: после незначительного количества итераций приходим к красивой шумной стабильной картинке, где нифига не понять.
– Сплайн-функцией горизонтальных, вертикальных и диагональных пикселей находятся 1, 2, 3. Значение пикселя 0 корректируется на основании того же постулата “среднее арифметическое 0, 1, 2 и 3 должно быть равно исходному значению 0”. Результат: при переходе от темной границы к светлой, цвет нулевого пикселя уходит в область отритцательных величин и утаскивает туда остальные.
Буду признателен за любые идеи и привлечение людей, знакомых с вопросом.
Принимаются даже очень экзотические варианты.
А можно жти два алгоритма описать для тупых на пальцах, ибо я вообще нихрена не понял как оно работает. От чего берётся среднее арифметическое? Что есть сплаин-функция? Откуда берётся исходное значение о?
Если второй алгоритм при переходе со светлого на темный работает приемлимо, не проще ли поставить умный итератор, который, работая с определенной частью картинки (3на3), выбирает, “с какой стороны работать”, с тем, чтобы переход всегда был со светлой на темную?
Тогда надо будет строить матрицу коэффициентов интерполяции на каждом шаге новую, а это жестокая трата ресурсов. У меня итак временная производительность алгоритма имеет порядок 6*n2